Die Modellierung und Berechnung komplexer Systeme und Zustandsänderungen mit herkömmlichen Methoden wie einer Fehlerbaumanalyse (FTA) stößt an ihre Grenzen, wenn stochastische Prozesse berücksichtigt werden müssen. In diesen Fällen ist es möglich, die Problemstellung mit Markov-Ketten darzustellen und die Wahrscheinlichkeit eines vorher definierten Systemzustandes (z.B. ein kritischer Fehlzustand) zu berechnen (Markov-Analyse).
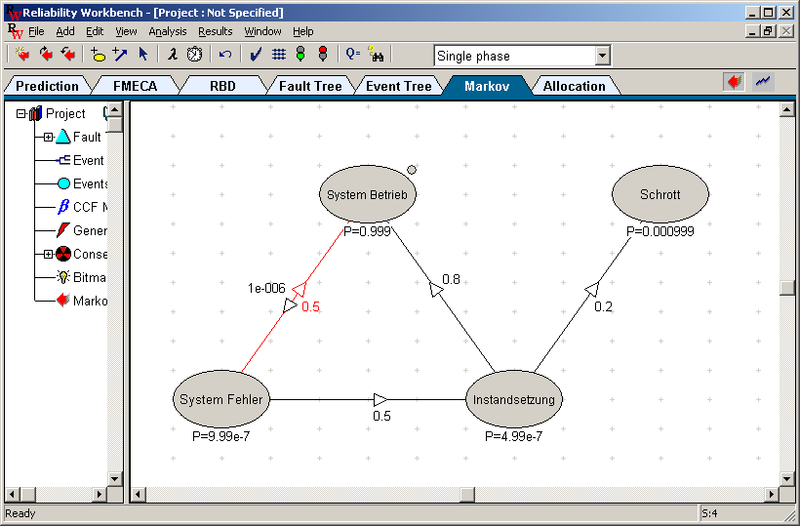
Bei der Modellierung mit Markov-Ketten werden die Systemzustände sowie die Übergänge der Zustände definiert. Hierbei sind auch Mehrfach- und Kreuzverbindungen zwischen den Zuständen möglich. Die für die Übergänge notwendigen Parameter (z.B. Fehlerrate, Verweildauer in einem Zustand, Reparaturzeit) werden ermittelt und bei der Berechnung berücksichtigt. Die Markov-Analyse berechnet auf der Basis dieser Parameter die Wahrscheinlichkeit für jeden definierten Systemzustand.
Das von uns eingesetzte Software-Tool FaultTree+ von Isograph Ltd. ermöglicht die Berechnung von Markov-Ketten und die Integration der Ergebnisse in die Fehlerbaumanalyse.
Mit der Markov-Analyse wird die Wahrscheinlichkeit für den Aufenthalt in einem definierten Systemzustand berechnet. Die Summe aller Wahrscheinlichkeiten ist dabei stets 1, da das System sich in einem der definierten Zustände befinden muss.
Die Markov-Analyse ermöglicht die Modellierung komplexer Funktionen und
Zusammenhänge im Rahmen
eines Sicherheitsprozesses. Häufig wird das
Ergebnis der Markov-Analyse zur Unterstützung einer Fehlerbaumanalyse dort eingesetzt, wo die Möglichkeiten der Fehlerbaumanalyse nicht
ausreichen, den Sachverhalt mit genügender Genauigkeit zu modellieren.

